Summary
The numerical modelling of fishing nets was the final project for my minor in Computational Science and Engineering. During this project, we developed a two-way non-linear cloth simulation, which was used to model the behaviour of fishing nets. The project was done in a team of 5 students, and I was responsible for the fluid simulation in OpenFOAM.
We developed a very computationally efficient simulation, which could to simulate a 3D fishing net with accurate correspondence to the literature. On the OpenFOAM side, I created a new OpenFOAM application to convert the output from the cloth simulation to a mesh suitable for OpenFOAM and to then convert the fluid simulation results back into pressures exerted onto the net. To do this, I generalised an approach in the literature to work for arbitrary net shapes while checking it still was identical in the simple case. Working on this project was a fun experience, and I learned a lot about OpenFOAM, using this experience to provide OpenFOAM workshops at the Robotics Student Association.


More details
Here, I will discuss some interesting aspects of the work I did for this project. I will begin by briefly discussing the net simulation side of the simulation to give a background on that part. After this, I will focus on the fluid simulation, starting with our literature study on porosity and the work of Chen et al. in 2016 [1], which provided the basis for our approach. I will then describe how I generalized the panel case to take into account volume, surface, and direction. Next, I will explain how I parallelized the computations to improve performance. Finally, I will compare our results to those found in the literature.
Nonlinear net solver
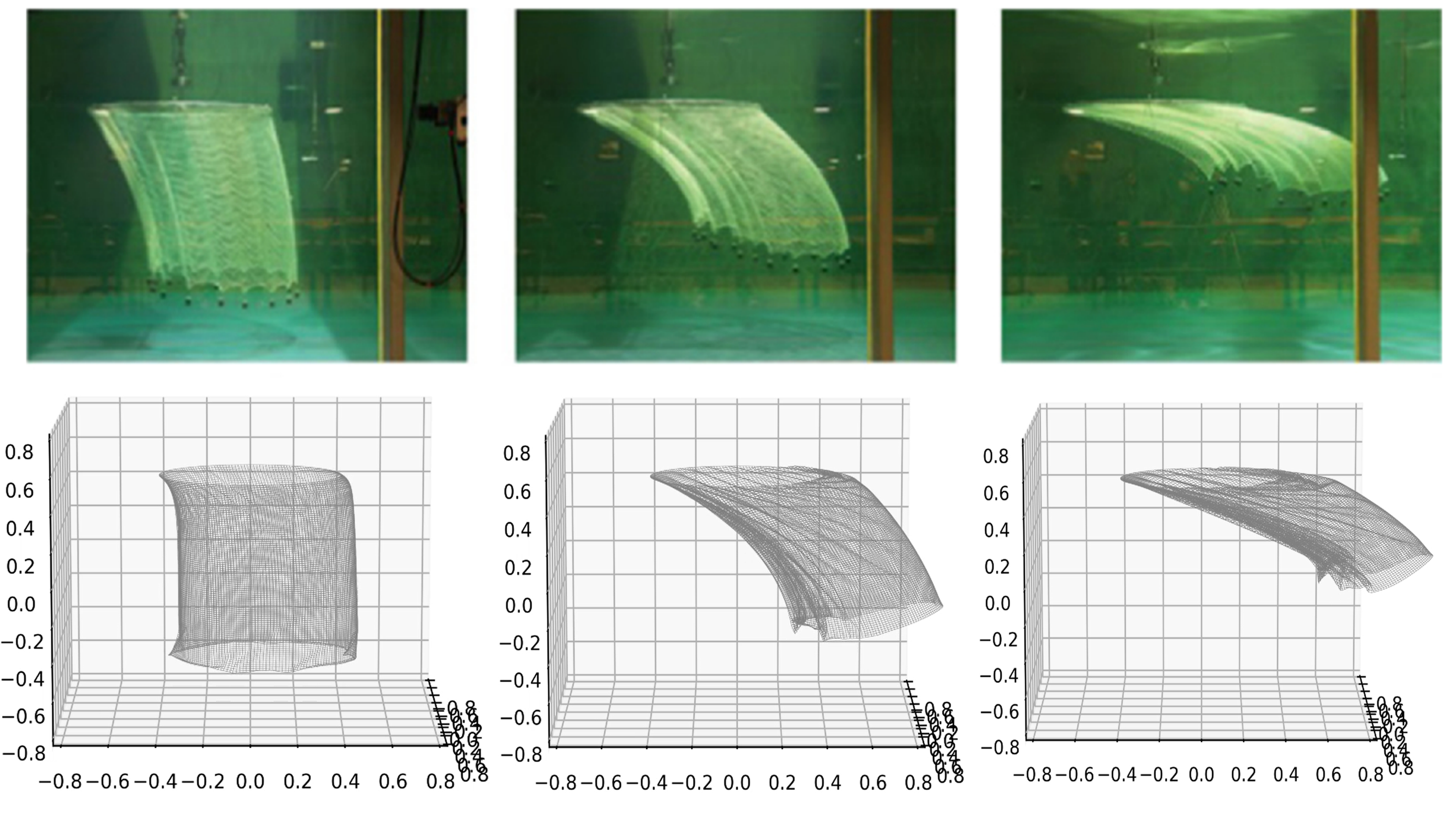
The net simulation was performed using a nonlinear cloth solver developed by other students on the team. The mass-spring model was based on the method proposed by Provot et al. (1995) [2] and initially assumed a steady, uniform flow to simulate the net behaviour. Later the net simulation could use the pressure fields computed by the fluid simulation to simulate the interaction with the fluid. Below is a figure which shows a qualitative comparison between the net simulation (without flow interactions) and experimental data by Chen et al. (2016) [1].
Simulating the net in a fluid
With the net simulation in place, we looked at methods to simulate the influence of the net on the fluid. We eventually settled on a method based on the work of Chen et al. (2016) [1], which was the most promising method we found in the literature for our limited computational power. The method is based on the idea that the net can be seen as a porous medium and that the pressure exerted by the fluid on the net can be computed by computing the momentum loss over the porous volume. The method essentially adds a momentum sink term to the incompressible Navier-Stokes equations in some regions of the mesh to model the presence of a porous region. This is known as the Darcy-Forchheimer equation; see [3].
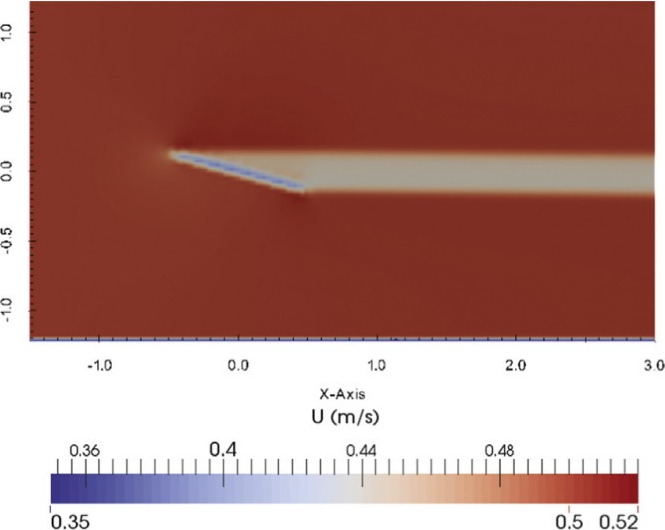
The method of Chen et al. (2016) [1] is only directly applicable to a simple case where the net has constant Darcy-Forchheimer coefficients (see the image to the right). However, we wanted to apply the method to a net with an arbitrary shape as simulated by the cloth solver. In the ideal case, the net would be represented in a complex OpenFOAM mesh with varying Darcy-Forchheimer coefficients in every cell. However, due to time (and experience) constraints, I chose to simplify the problem to a case where the full net shape is represented by a set of panels which behave exactly as those in the method of Chen et al. This process is described in more detail below.
Generalising the panel case
For the panel case to be generalised, I needed to find a way to compute the Darcy-Forchheimer coefficients for each porous region representing a single panel. This was done by generalising the coefficient calculation to arbitrary geometries, considering the panel's volume, surface, and direction. The volume and surface of the porous region were computed by integration over the relevant parts over the mesh. Calculating the volume for these regions in that way was trivial but calculating the projected surface area was more difficult. The images below represent the surface calculation process for a single panel. In these images, the cells represent the porous region, and the plane represents the panel.
The projected surface area of the porous region is calculated by taking the dot product of the normal vector of the panel and the normal vector of every cell face and then integrating this over all the cell faces. The result is shown in the right image, where the black outline is the outline of the projected area using this method. The red areas represent a small error in calculating the areas this way. These areas are counted twice in the final result. This is because calculating the projected area with integration like this assumes that the porous region has a convex shape, but that may not always be guaranteed (such as in this example). However, this remains a reasonable assumption for the panels as the error is small relative to the total area, given that this error also decreases when the resolution of the mesh is increased.
The results of the above method are shown in the figures below. Here the case from Chen et al. (2016) [1] is recreated, but now no manual input of the Darcy-Forchheimer coefficients is required. This method now also allows for easily changing the mesh resolution as the coefficients are computed automatically using the volume and the projected area of the porous region.
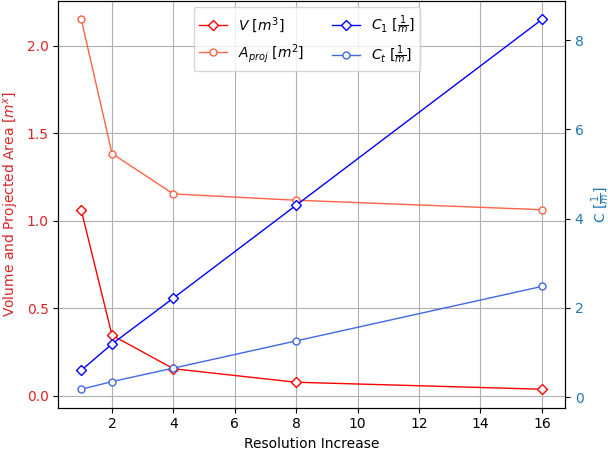
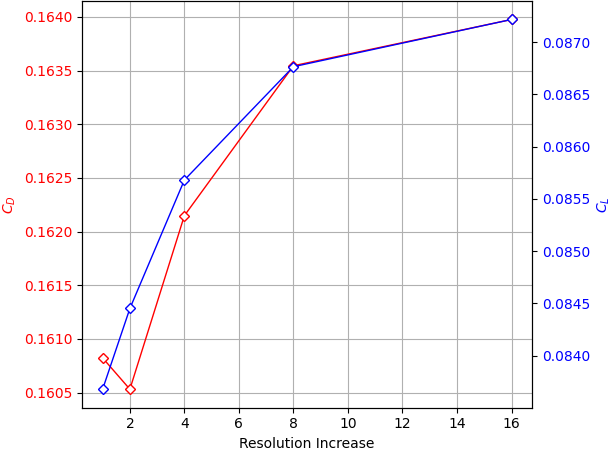
The image on the left shows a panel represented by a high-resolution porous region in black and a low-resolution porous region in white. The image in the middle then shows the Darcy-Forchheimer as a function of this resolution and the image on the right shows the sensitivity of the drag and lift coefficients to the resolution. These results show that the panel simulation is not sensitive to the mesh resolution, only varying by a few percent over a sixteen-fold resolution increase. This is good news for the computational intensity of the method. These lift and drag coefficients also correspond exactly with the same case's results from Chen et al. (2016) [1]. This correspondence shows that the method is working as intended.
Parallelizing and computational resources
All of the above, including the solvers, had to be executed on our laptops, meaning we quickly ran into performance and storage bottlenecks. Because the simulations took too long to complete for iteration on the results, we decided to look into parallelizing the entire procedure. This was also surprisingly required for the prerprocessing and postprocessing of the results, which took almost as much computation as the fluid simulation itself. Implementing the parallelization broke a lot of our approach in the last weeks before the deadlines because of the large changes to mesh and file structures in the OpenFOAM frontend. This meant that we had to reverse engineer a lot of the parallelization performed by OpenFOAM and then refactor our solution.
On top of this, the project was completed during COVID, which meant a purely online work environment. The ensuing cocktail of gigantic file transfers, different program environments and operating systems made the project a great lesson in flexibility and adaptability.
Correspondence with literature
Despite the above troubles, our results still corresponded very well with the literature. For example, the image below shows the simulation of a net configuration described in the work of Tang et al. (2019) [4], where the Vertical Opening Ratio (VOR) describes how much the net opens under a particular flow. In the figure on the right, it can be seen that the VOR, as simulated by our method, follows a similar power law as obtained by Tang et al. (2019) [4].
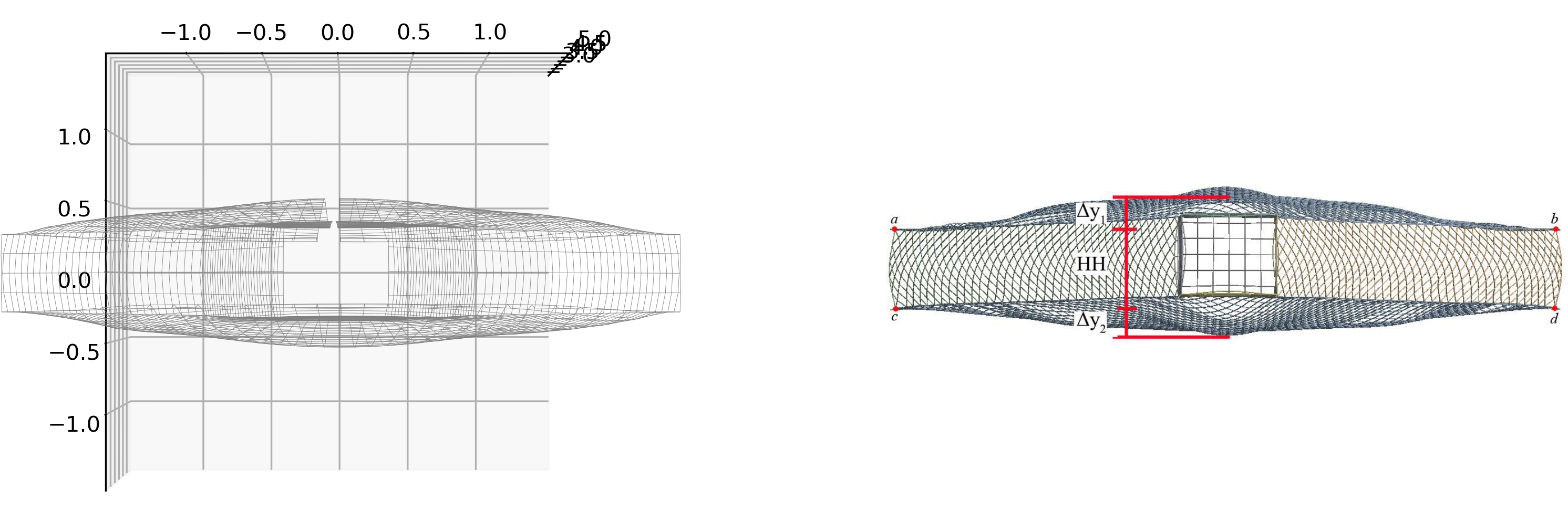
Studying the convergence of the full net simulation, a slightly worrying trend was observed. The figure below shows the drag coefficient and simulated velocities at several stations in the net as a function of the resolution of the mesh. It can be seen in this figure that slow convergence to steady values is present. However, we could not increase the resolution of our simulation far enough to observe the convergence to the final values. This is in stark contrast to the simple panel case, which was not sensitive to the mesh resolution at all.
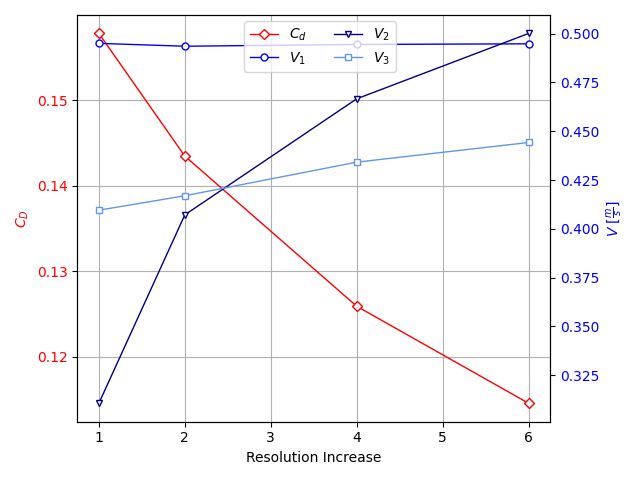
We hypothesized that this is because the net, in this case, was not a simple geometry. This means that increasing the mesh resolution can have nonlinear effects on the flow. An example of a complex net configuration with effects like this would be the case of a net with a modest opening in the middle. At a certain low resolution, this opening would not be resolved anymore by the mesh, and this would lead to a drastically different flow field. However, as we observed, in simple cases it is possible to get very far with only simple simulation steps. In some instances, it was even observed that the pure cloth simulation without the fluid simulation in the loop could have significant predictive power. This was in situations where the assumption of a steady uniform flow, as made by the cloth model, was valid.
My experience working on the project
Working on this project was an outstanding experience; we had a great team and tutors. I had to pick up the usage and development for OpenFOAM in a short amount of time, together with all the complications of running it with the windows subsystem for Linux in VS Code. After this project, I went on to use OpenFOAM in other projects and taught it to others at the RSA in workshops.
References
- [1] H. Chen, E.D. Christensen, ”Investigations on the Porous Resistance Coefficients for Fishing Net Structures”, Journal of Fluids and Structures, Vol. 65, pp. 76-107 (2016)
- [2] H. Provot, ”Deformation Constraints in a Mass-Spring Model to Describe Rigid Cloth Behaviour”, Proceedings of Graphics Interface, pp. 147-154, https://doi.org/10.20380/GI1995.17. (1995)
- [3] OpenCFD Ltd, "The Darcy-Forchheimer Equation" https://openfoamwiki.net/index.php/DarcyForchheimer
- [4] M.F. Tang, G.H. Dong, T.J. Xu, Y.P. Zhao, ”Numerical Simulation of the Drag Force on the Trawl Net”, Turkish Journal of Fisheries and Aquatic Sciences, Vol. 17, pp. 1219-1230 (2017)